Solve for y when x = –1" Now you say "f (x) = 2x 3;Something went wrong Wait a moment and try again Try again0 < C < 1 compresses it;

7 1 What Does Fx Mean Youtube
Meaning of f x y
Meaning of f x y-If y(x) = 2x, that means that for every incremental increase in x, y increases by 2 increments Y is twice the value of x, for every value x takes on If x = 5, then y = 2 x 5 = 10 If x = 02, then y = 2 x (02) = 04 Y isn't always (or even usually) a function of just one variable Y can vary according to an infinite number of variablesC < 0 moves it down;




Meaning Is The Value Assumed By F X In The Codomain Y Download Scientific Diagram
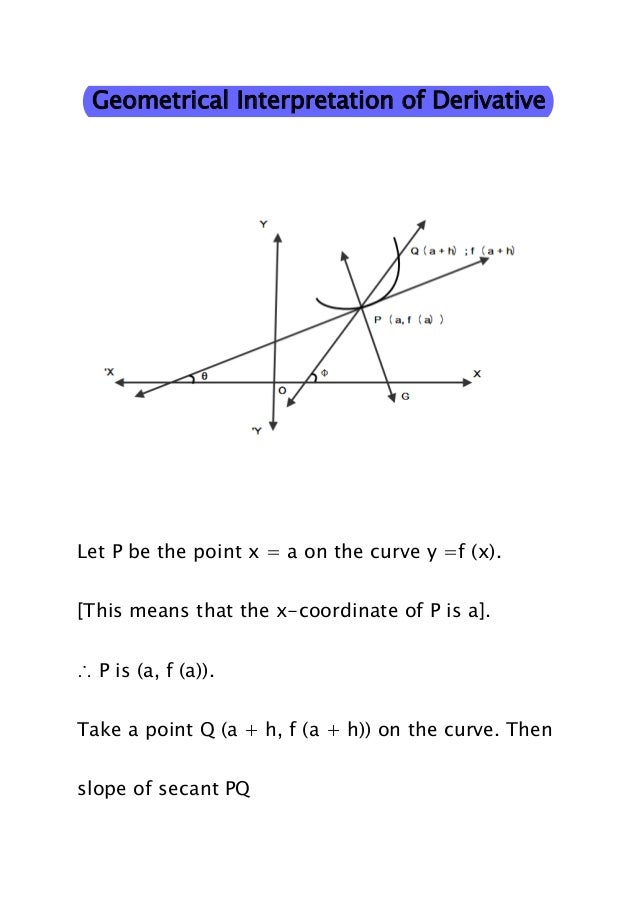
Y = f(−x) Reflects it about yaxisThe function f(x,y) is a bivariate function;The derivative of a function y = f(x) of a variable x is a measure of the rate at which the value y of the function changes with respect to the change of the variable x It is called the derivative of f with respect to x If x and y are real numbers, and if the graph of f is plotted against x, derivative is the slope of this graph at each point
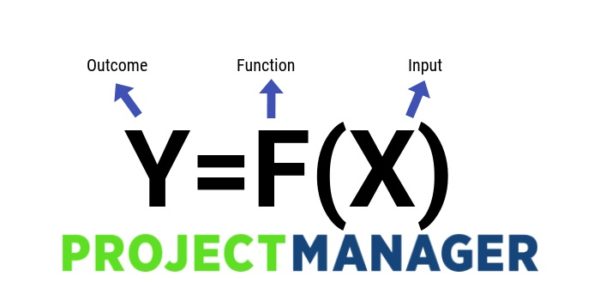
The same is true of "y" and "f (x)" (pronounced as "effofeks") For functions, the two notations mean the exact same thing, but "f (x)" gives you more flexibility and more information You used to say "y = 2x 3;Free maths videos at http//sickmathscomIn the strictest view, Y=f (x) is a representation of a mathematical formula It is one to use when examining different possible outcomes based on the inputs and factors used The "Y" stands for the outcome, the "f" embodies the function used in the calculation, and the "X" represents the input or inputs used for the formula
we mean the derivative of the function f(x) with respect to the variable x One type of notation for derivatives is sometimes called prime notation The function f´(x), which would be read ``fprime of x'', means the derivative of f(x) with respect to x If we say y = f(x), then y´ (read ``yprime'') = f´(x)We set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x cannot be equal to 2 or 0 Please click on the image for a better understandingF (X) ε All of Six Sigma can be summarized with what's called the breakthrough equation — one generalpurpose equation that shouldn't intimidate even the least mathematically inclined Y = f ( X) ε, where Y is the outcome (s) or result (s) you desire or need X represents the inputs, factors, or pieces necessary to create the



Search Q Mean Formula Tbm Isch




6 Ways To Find The Domain Of A Function Wikihow
Y = f(Cx) C > 1 compresses it in the xdirection;Means that every element in X is related to some element in Y We say that the function covers X (relates every element of it) (But some elements of Y might not be related to at all, which is fine)It is a different way of writing "y" in equations, but it's much more useful!




Consider The Following Information 1 Y F X 2 Chegg Com




Pin On Differential Equations
Looking for online definition of F/Y or what F/Y stands for?Y=f of x flips the graph across the x axis But how do you reflect it across the y axis? f (x,y,z) is a function in x,y and z In R 3, the function lies in all three planes so to speak The domain of a function of three variables is R 3 or a subset of it The graph of w = f (x, y, z) is the set of ordered quadruples (x, y, z, w) such that w = f (x, y, z) Such a graph requires four dimensions three for the domain and one for the



Derivatives And Their Real World Applications




Ppt Nicolina A Malara Mathematics Department Modena Reggio E University Italy Powerpoint Presentation Id 7590
In this video I try to explain what a function in maths is I once asked myself, why keep writing y=f(x) and not just y!??Math Central I find it helps sometimes to think of a function as a machine, one where you give a number as input to the machine and receive a number as the output The name of the function is the input is x and the output is f (x), read " f of x"'f' represents the nature and strength of the relationship that exists between Y and X On one hand, this equation can be used for a generic interpretation that symbolizes the fact that Y is impacted by X




The Graph Of The Equation Examples Solutions Videos Worksheets Homework Lesson Plans




What S The Meaning Of Tilde Y Mathematics Stack Exchange
Y=f (X) is one of many types of transfer functions In a nutshell, a transfer function, as defined by Mathworks, is a "convenient way to represent a linear, timeinvariant system in terms of its inputoutput relationship" Most of us are probably comfortable with the terms linear, input, and output But, what does "timeinvariant" mean?F/Y is listed in the World's largest and most authoritative dictionary database of abbreviations and acronyms F/Y What does F/YThat means f is defined over two independent variables x and y For easier imagination, consider z=f(x,y) in the x,y,z coordinate system Let's define z=x^2 y^2 = f(x,y) For z=0, x^2 y^2 = 0 represe




Meaning Of Phi In Spivak S Proof Of Inverse Function Theorem Mathematics Stack Exchange



F X Math
What does f in Y= f(X) mean?What does y= f (x) actually mean?And, at each point, it computes f of x, y at the point, finds, meets, and computes the value of f of (x, y), that function, and the next thing is, on the screen, it draws, at (x, y), the little line element having slope f of x,y In other words, it does what the differential equation tells it to do



Injective Function Wikipedia




Chapter 2 Calculus Hugheshallett The Derivative Continuity Of
Cauchy's functional equation is the functional equation () = () Solutions to this are called additive functionsOver the rational numbers, it can be shown using elementary algebra that there is a single family of solutions, namely ↦ for any rational constant Over the real numbers, the family of linear maps ↦, now with an arbitrary real constant, is likewise a family of solutionsFor the usual y = f(x), the input is x and the output is y For the INVERSE function x = f^1(y), the input is y and the output is x If y equals x cubed, then x is the cube root of y that is the inverse If y is the great function e^x, then x is the NATURAL LOGARITHM ln y Start at y, go to x = ln y, then back to y = e^(ln y) A major advantage provided by the implementation of Six Sigma is changing the thought process from trial and error to Y = f (x) Most training programs for Six Sigma seem to focus on teaching the tools rather than driving home the importance of scientific problemsolving for process improvement That is where breakthroughs really begin




Symmetric About The Y Axis Functions Symmetric About




Fixing The Symptoms Y F X Straightup Forum
The statement y = f ( x) is just a condition for some set of points (ie ( x, y) pairs) while y = g ( x) is another condition for another set of points Explicit definition in a form y ( x) = does define a function (well, does or doesn't, read the next paragraph) In this case y is just an arbitrary name and may replace fY = f(x) y is a function of x d Notice a most important fact y and f(x) may be used interchangeably; This formula is especially relevant to determining cause and effect as well as measuring for improvement It reads Y is a function of X The Y is the effect of the problem or desired improvement and the X's are the possible causes or areas affecting improvement



Shifting And Stretching Graphs The Math Doctors




1 Explain In Your Own Words The Meaning Of Each Of Chegg Com
The notation y = y ( x) is overloaded as y can now be used to refer both to a function y D → C and a variable y ∈ C This is a dangerous practice which can cause students a world of pain Consider the following elementary application of the chain rule Let f R 2 → R, x, y R → R be differentiable, and consider the function z RY = f(x C) C > 0 moves it left;Y=fx for project management in a nutshell and high level is a common principal used when managing project of any type If you want a deeper meaning take a look at this post What Does Y=f (X) Mean Regarding Project Management?




What Is Difference Between Math X F Y Math And Math Y F X Math Graph Quora



12th Maths Geometrical Interpretation Of Derivatives Jee Main 1
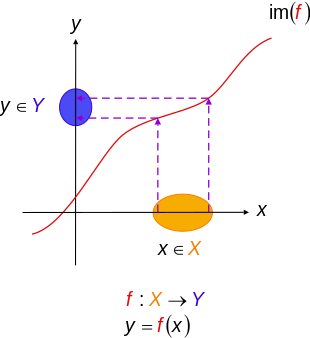
In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);The fact of f being a function from the set X to the set Y is formally denoted by f X→Y In the definition of a function, X and Y are respectively called the domain and the codomain of the function f If (x, y) belongs to the set defining f, then y is the image of x under f, or the value of f applied to the argument xY = −f(x) Reflects it about xaxis;




1 Transformations Of Functions Section Learn The Meaning Of Transformations Use Vertical Or Horizontal Shifts To Graph Functions Use Reflections Ppt Download




How To Evaluate A Function Function Notation Input Output Visual Examples And Explained Problems Math Warehouse
Well instead of flipping the y values, you want to flip the x values So you replace the x with minus x and that will reflect the graph across the y axis So let's consider an example y=2 to the negative x This is a reflection of what parent function? Y = f (x) Process Outcome a Result of Process Inputs The mathematical term Y = f (x), which translates as simply " Y is a function of x," illustrates the idea that the important process outcomes ( Y s) are a result of the drivers ( x 's) within processes The goal of DMAIC is to identify which few process and input variables mainlyC < 0 moves it right;



What S Does Y F X Mean How To Use This Powerful Six Sigma Formula




Part A Ordinary Differential Equations Odes Section 1
Find f (–1)" (pronounced as "fofx equals 2x plus three;Y = Cf(x) C > 1 stretches it in the ydirection; lim x→a−f (x) lim x → a − f ( x) is a left hand limit and requires us to only look at values of x x that are less than a a In other words, we will have lim x→af (x) =L lim x → a f ( x) = L provided f (x) f ( x) approaches L L as we move in towards x =a x = a (without letting x = a x = a) from both sides




Unit2 Multiple Random Variable N N N N
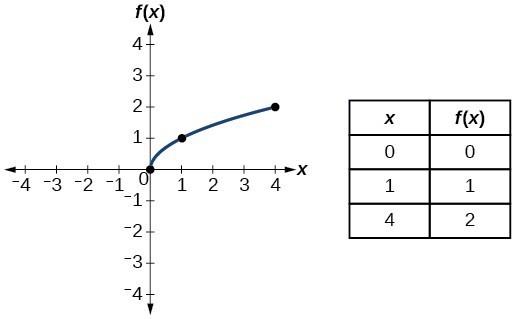



Characteristics Of Functions And Their Graphs Lumen Learning College Algebra
The rate of change of f (x,y) f ( x, y) in the direction of the unit vector →u = a,b u → = a, b is called the directional derivative and is denoted by D→u f (x,y) D u → f ( x, y) The definition of the directional derivative is, D→u f (x,y) = lim h→0 f (x ah,y bh)−f (x,y) h D u → f ( x, y) = lim h → 0 They both mean what you get back after you have chosen a particular x value e Let s look at both the old way and the new way of notating some values of x and y which satisfy our equation of yIn this video we learn about function composition Composite functions are combinations of more than one function In this video we learn about f(g(x)) and g



Operations On Functions Stretches And Shrinks Sparknotes




Integrative Writing Assignment Derivative The Chegg Com
Y = f(x) C C > 0 moves it up; In this section the subscript notation f y denotes a function contingent on a fixed value of y, and not a partial derivative Once a value of y is chosen, say a, then f(x,y) determines a function f a which traces a curve x 2 ax a 2 on the plane =I've since realised that 'y' can b
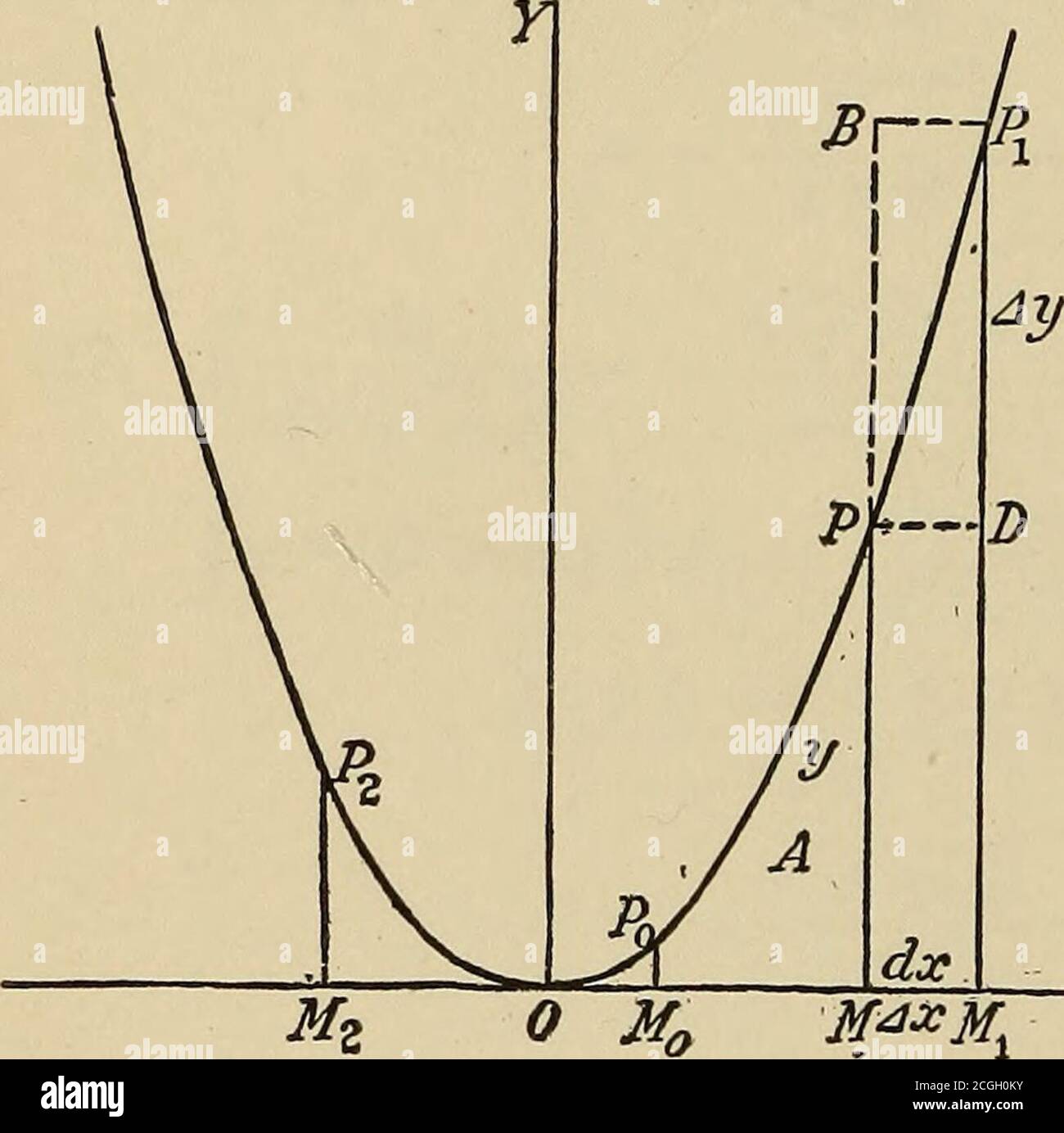



Applied Calculus Principles And Applications E Integrals Areas 125 Geometric Meaning Of X Dx As The Repre Sentation Of An Integral By An Area Between A Curve And




Meaning Is The Value Assumed By F X In The Codomain Y Download Scientific Diagram
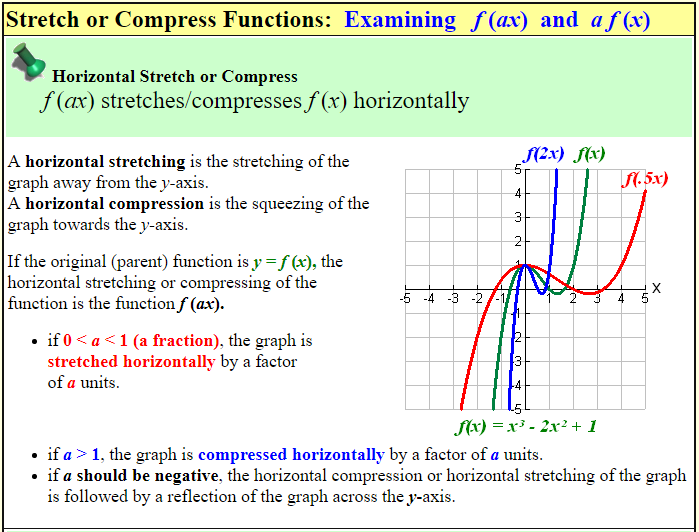
0 < C < 1 stretches it;In mathematics, the exponential function is the function f ( x ) = e x, {\displaystyle f(x)=e^{x},} where the base e = 2718 is Euler's number and the argument x occurs as an exponent More generally, an exponential function is a function of the form f ( x ) = a b x, {\displaystyle f(x)=ab^{x},} where the base b is a positive real number For real numbers c and d, a function of the form f ( x ) = a b c x d {\displaystyle f(xThe parameter a can be added to or subtracted from the input x before the rule f is applied y = f(x) becomes y = f(x ± a) These transformations are called horizontal shifts or translationsThey move the graph of the given function left (adding positive a) or right (subtracting positive a)




7 1 What Does Fx Mean Youtube




Examples Of The Types Of Questions On The Left Side A Conceptual Download Scientific Diagram
The phrase "y is a function of x" means that the value of y depends upon the value of x, so y can be written in terms of x (eg y = 3x) If f (x) = 3x, and y is a function of x (ie y = f (x)), then the value of y when x is 4 is f (4), which is found by replacing x"s by 4"sGiven an equation tell whether y is a function of x We discuss different ways of deciding whether for every input there is exactly one output We go over




2 1 Introduction To Limits Ppt Download




Problem 2 10pts Sketch The Graph Of The Function Y Chegg Com



If Y F F X And F 0 0 F 0 5 Then What Is Dy Dx X 0 Quora




Suppose F X Y Is A Function Of Two Variables X And Chegg Com



Operations On Functions Stretches And Shrinks Sparknotes




Let F X Xe 6x A Find The Values Of X For Which Chegg Com




Function Mathematics Wikipedia



The Reflection Y F X Youtube




2 For A Function F X Which Is A Probability Density Chegg Com



Meaning Of A Vertical Bar In Differentiation Pytorch Forums




The Formula Y Fx X F Models The Relationships Needed To Focus An Image Where Y Is The Distanc Homeworklib




Plots Of Sample Mean Of A Y I F Against Y I F X And B Y I G Download Scientific Diagram
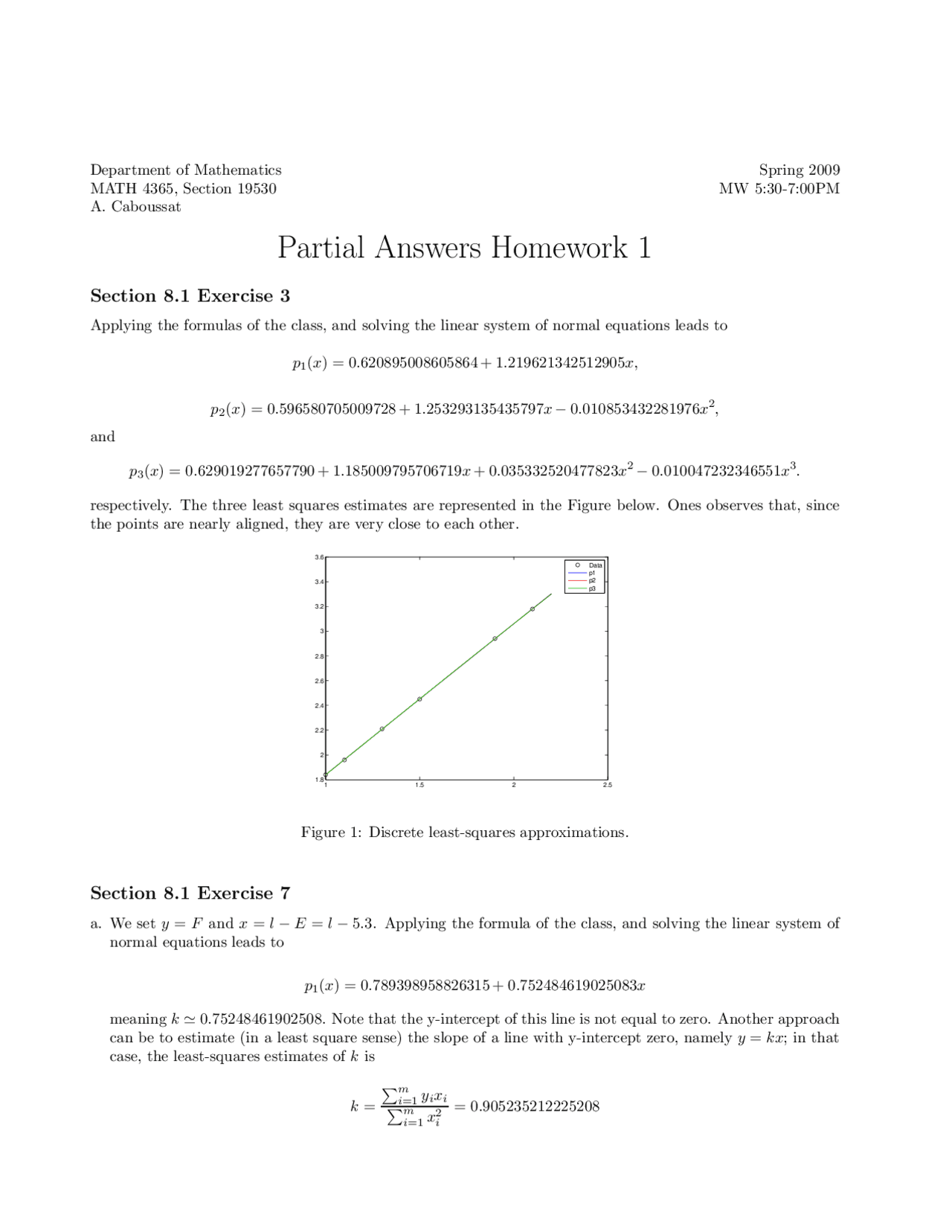



Answers For Homework 1 Numerical Analysis Math 4365 Docsity




Denotational Semantics Denotational Semantics Ppt Download




It X 1 Consider The Function F X Y Ja2 0 If Chegg Com
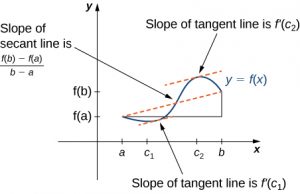



4 1 Applications Of 1st Derivative Techniques Of Calculus 1



All Elementary Mathematics Study Guide Principles Of Analysis Derivative Geometrical And Mechanical Meanings Of Derivative
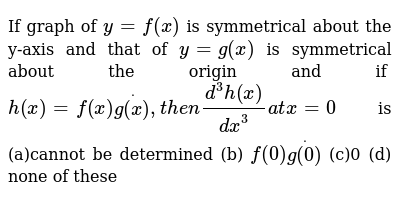



If Graph Of Y F X Is Symmetrical About The Y Axis And That
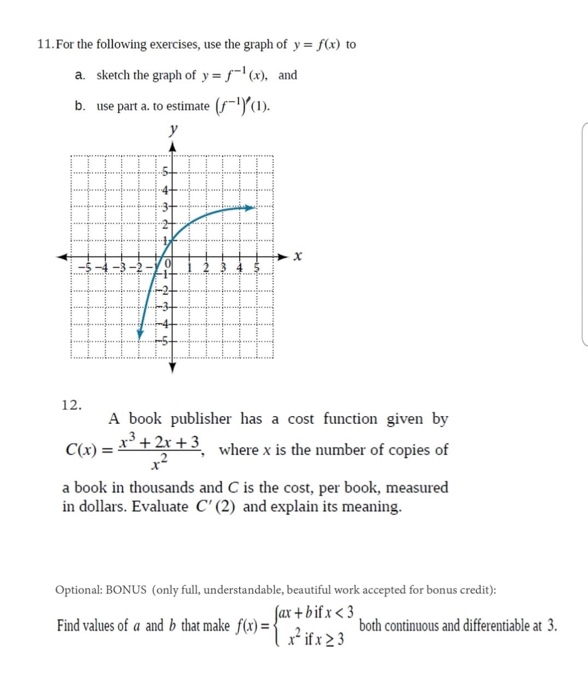



11 For The Following Exercises Use The Graph Of Y Chegg Com
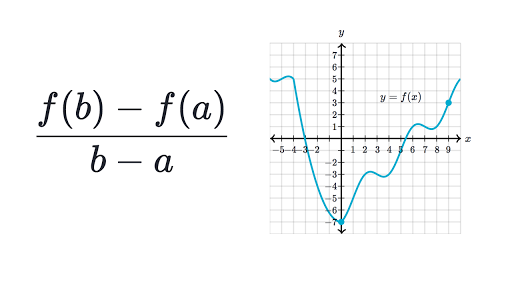



Average Rate Of Change Review Article Khan Academy




Examples Of The Types Of Questions On The Left Side A Conceptual Download Scientific Diagram




Numerical Methods And Analysis Nma 312 Prof Samuel




6 Ways To Find The Domain Of A Function Wikihow




6 Ways To Find The Domain Of A Function Wikihow




Differential Calculus Wikiwand




Class X Ch2 Polynomials Part 1 On Vimeo



Search Q Function Tbm Isch




5 3 Inverse Functions Mathematics Libretexts




If The Graph Of A Function F X Is Symmetrical About The Line X A Then



Answered Define The Physical Meaning Of Curl F Bartleby




Solved Use Definition 2 2 1 To Find F Prime X And Then Find The Tangent Line To The Graph Of Y F X At X A F X




What Does F X Mean Youtube




Differential Calculus Of The Function Of One Variable Online Presentation




What Does Y Is A Function Of X In Real Life Mean Quora




The Triple Integral Properties Of Triple Integrals The Calculation Of The Triple Integral And Volumes Of Solids Prezentaciya Onlajn



Inflection Points



Search Q Interval Notation Tbm Isch




The Chain Rule Harvey Mudd College Department Of Mathematics




Prove That If B Is A Domain In R 2 Symmetric Relative Chegg Com
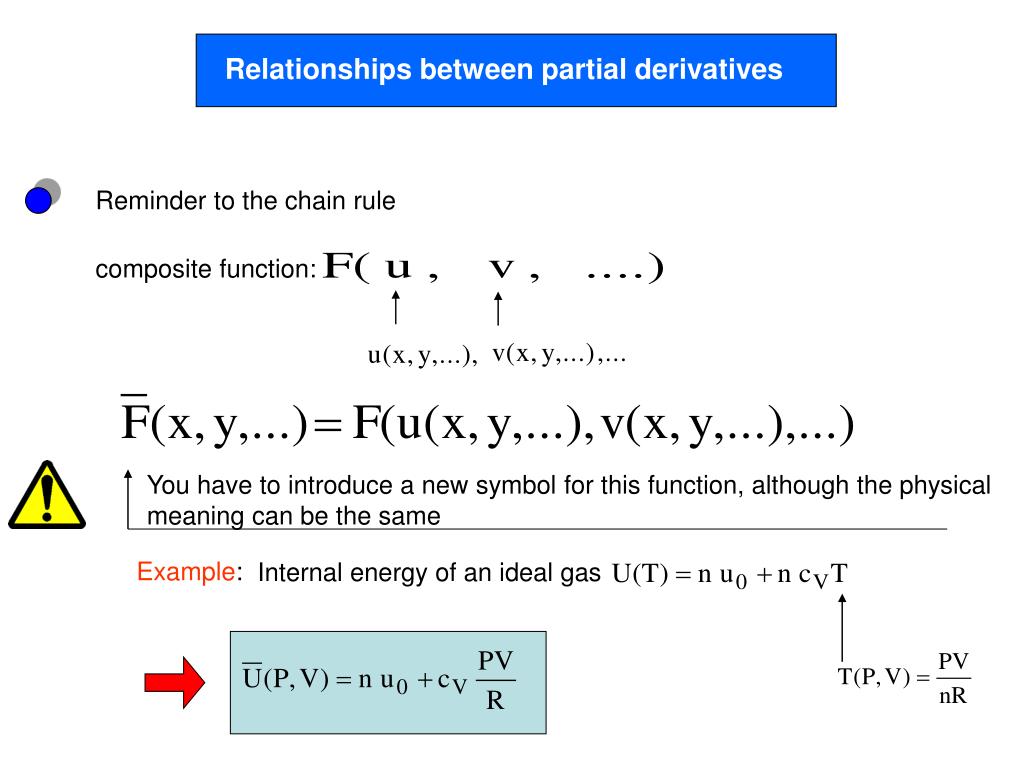



Ppt Relationships Between Partial Derivatives Powerpoint Presentation Id



Http Www Kkuniyuk Com Calcbook Calcnotes08 Pdf




Quadratic Function Wikipedia




14 Bpts Consider An Agricultural Production Function Y F Kl Where Is The Number Of Units Homeworklib




The Derivative Of The Function Y F X At X 3 Is Chegg Com




4 1 And 4 6 Deriv Meaning And Local Linearity Youtube




Square Root Wikipedia




Yfx Y F X Ax Ay Ax H Ax X X The Meaning Of The Derivative An Approach To Calculus Meaning Meme On Me Me




Xy X2 If X Y 0 0 Consider The Function F X Y Chegg Com




Using Function Notation What Is F X Youtube




Calculating The Derivative Notations For The Derivative The Derivative Of Y F X May Be Written In Any Of The Following Ways You Need To Become Ppt Download




Maths What Is A Function Y F X Youtube




Answered Suppose An Extremal Value Of F Occurs Bartleby
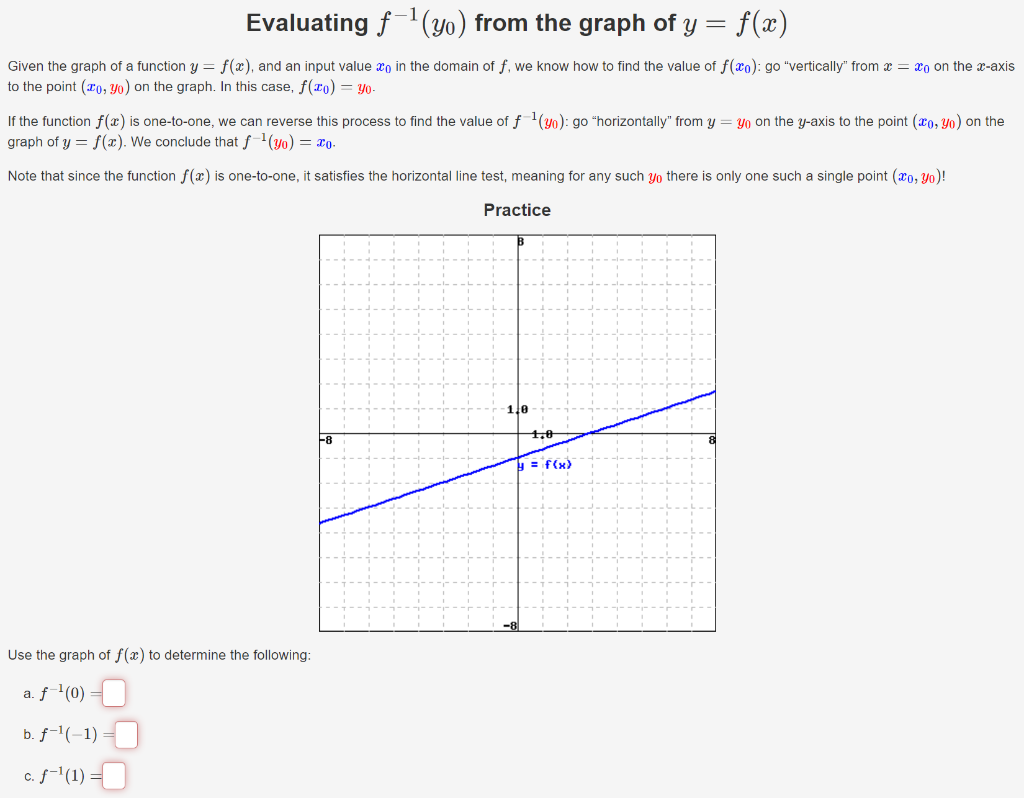



Evaluating F L Yo From The Graph Of Y F X Given Chegg Com




F X Meaning




Geometrical Meaning Of Differentiability Youtube




Question 5 2 Points From The Following Chart Choose Chegg Com




Differential Calculus Of The Function Of One Variable Prezentaciya Onlajn




3 Derivatives Derivatives We Have Seen That A




What Is The Meaning Of A Differential In Terms Of An Exact Differential Mathematics Stack Exchange




Model 1 Guessing A Limit Of A Function From A Graph Chegg Com
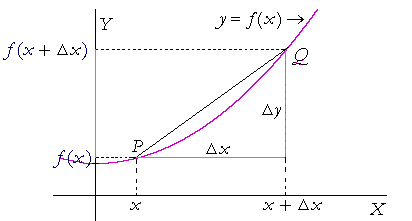



Fx Meaning Math Forex Trading And Taxes
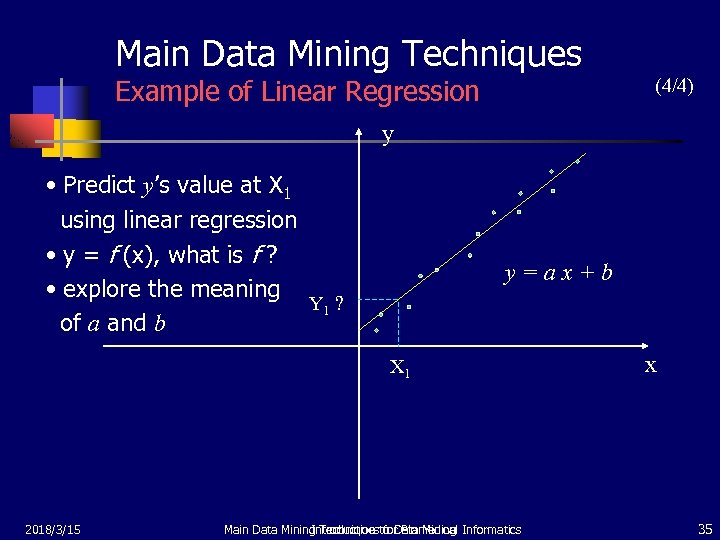



Chapter 1 Introduction To Data Mining Chen Chun Hsien




Function Mathematics Wikipedia




1 Explain In Your Own Words The Meaning Of Each Of Chegg Com
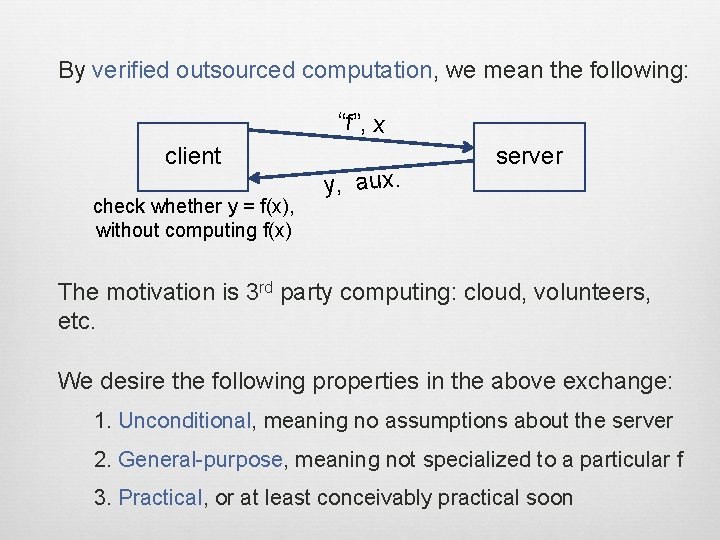



Making Argument Systems For Outsourced Computation Practical Sometimes




3 1 Derivative Of A Function Ppt Download




Meaning Of Phi In Spivak S Proof Of Inverse Function Theorem Mathematics Stack Exchange




1 1 Section 1 1 P 1 Basic




A Toy Illustration Of The Meaning Of Highprobability Safety Guarantees Download Scientific Diagram




Do Now 11 10 09 Copy Hw In Your Planner Copy Hw In Your Planner Text P 266 4 34 Even 38 In Your Notebook Explain In Your Own Words The Meaning Ppt Download




Warm Up 10 Min I Factor The Following Expressions Completely Over The Real Numbers 3x3 15x2 18x X4 X2 Ii Solve Algebraically And Graphically Ppt Download




Why Is Calculus Important Central Mathematical Subject Underpinning Science And Engineering Central Mathematical Subject Underpinning Science And Engineering Ppt Download




Y F X Meaning



Yfx Fox Harbour St Lewis Nf Fox Harbour Aerodrome Canada By Acronymsandslang Com



No comments:
Post a Comment